题目描述
2048年,第三十届 CSP 认证的考场上,作为选手的小明打开了第一题。这个题的样例有n组数据,数据从1∼n标号,i号数据的规模为ai。
小明对该题设计出了一个暴力程序,对于一组规模为u的数据,该程序的运行时间为u2。然而这个程序运行完一组规模为u的数据之后,它将在任何一组规模小于u的数据上运行错误。样例中的ai不一定递增,但小明又想在不修改程序的情况下正确运行样例,于是小明决定使用一种非常原始的解决方案:将所有数据划分成若干个数据段,段内编号连续,接着将同一段内的数据合并成新数据,其规模等于段内原数据的规模之和,小明将让新数据的规模能够递增。
也就是说,小明需要找到一些分界点1≤k1<k2<⋯<kp<n,使得
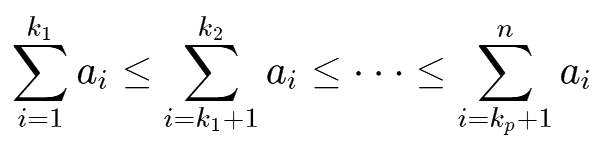
注意p可以为0且此时k0=0,也就是小明可以将所有数据合并在一起运行。
小明希望他的程序可以在正确运行样例情况下, 运行时间也能尽量小,也就是最小化
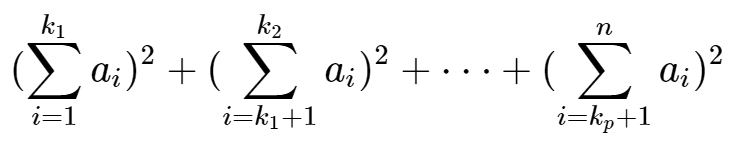
小明觉得这个问题非常有趣,并向你请教:给定n和ai,请你求出最优划分方案下,小明的程序的运行时间。
小明对该题设计出了一个暴力程序,对于一组规模为u的数据,该程序的运行时间为u2。然而这个程序运行完一组规模为u的数据之后,它将在任何一组规模小于u的数据上运行错误。样例中的ai不一定递增,但小明又想在不修改程序的情况下正确运行样例,于是小明决定使用一种非常原始的解决方案:将所有数据划分成若干个数据段,段内编号连续,接着将同一段内的数据合并成新数据,其规模等于段内原数据的规模之和,小明将让新数据的规模能够递增。
也就是说,小明需要找到一些分界点1≤k1<k2<⋯<kp<n,使得
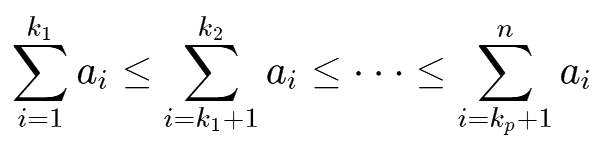
注意p可以为0且此时k0=0,也就是小明可以将所有数据合并在一起运行。
小明希望他的程序可以在正确运行样例情况下, 运行时间也能尽量小,也就是最小化
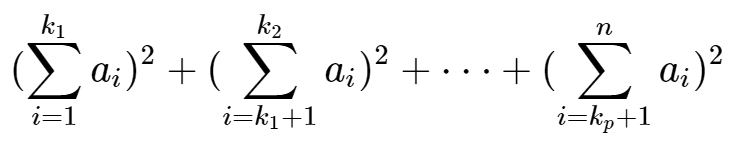
小明觉得这个问题非常有趣,并向你请教:给定n和ai,请你求出最优划分方案下,小明的程序的运行时间。
输入
由于本题的数据范围较大,部分测试点的ai将在程序内生成。
第一行两个整数n,type。n的意义见题目描述,type表示输入方式。
若type=0,则该测试点的ai直接给出。输入文件接下来:第二行n个以空格分隔的整数ai,表示每组数据的规模。
若type=1,则该测试点的ai将特殊生成,生成方式见后文。输入文件接下来:第二行六个以空格分隔的整数x,y,z,b1,b2,m。接下来m行中,第 i(1≤i≤m) 行包含三个以空格分隔的正整数pi,li,ri。
对于type=1的23∼25号测试点,ai的生成方式如下:
给定整数x,y,z,b1,b2,m,以及m个三元组 (pi,li,ri)。
保证n≥2。若n>2,则 ∀3≤i≤n,bi=(x×bi−1+y×bi−2+z)mod230。
保证1≤pi≤n,pm=n。令p0=0,则pi还满足 ∀0≤i<m有pi<pi+1。
对于所有1≤j≤m,若下标值 i(1≤i≤n) 满足 pj−1<i≤pj,则有
ai=(bi mod(rj−lj+1))+lj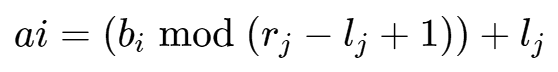
上述数据生成方式仅是为了减少输入量大小,标准算法不依赖于该生成方式。
第一行两个整数n,type。n的意义见题目描述,type表示输入方式。
若type=0,则该测试点的ai直接给出。输入文件接下来:第二行n个以空格分隔的整数ai,表示每组数据的规模。
若type=1,则该测试点的ai将特殊生成,生成方式见后文。输入文件接下来:第二行六个以空格分隔的整数x,y,z,b1,b2,m。接下来m行中,第 i(1≤i≤m) 行包含三个以空格分隔的正整数pi,li,ri。
对于type=1的23∼25号测试点,ai的生成方式如下:
给定整数x,y,z,b1,b2,m,以及m个三元组 (pi,li,ri)。
保证n≥2。若n>2,则 ∀3≤i≤n,bi=(x×bi−1+y×bi−2+z)mod230。
保证1≤pi≤n,pm=n。令p0=0,则pi还满足 ∀0≤i<m有pi<pi+1。
对于所有1≤j≤m,若下标值 i(1≤i≤n) 满足 pj−1<i≤pj,则有
ai=(bi mod(rj−lj+1))+lj
上述数据生成方式仅是为了减少输入量大小,标准算法不依赖于该生成方式。
输出
输出一行一个整数,表示答案。
样例输入 Copy
5 0
5 1 7 9 9
样例输出 Copy
247
提示
样例1
input
5 0 5 1 7 9 9
output
247
explanation
最优的划分方案为 {5,1},{7},{9},{9}。由5+1≤7≤9≤9知该方案合法。
答案为 (5+1)2+72+92+92=247。
虽然划分方案 {5},{1},{7},{9},{9} 对应的运行时间比 247小,但它不是一组合法方案,因为5>1。
虽然划分方案 {5},{1,7},{9},{9} 合法,但该方案对应的运行时间为251,比 247大。
样例2
input
10 0 5 6 7 7 4 6 2 13 19 9
output
1256
explanation
最优的划分方案为 {5},{6},{7},{7},{4,6,2},{13},{19,9}。
样例3
input
10000000 1 123 456 789 12345 6789 3 2000000 123456789 987654321 7000000 234567891 876543219 10000000 456789123 567891234
output
4972194419293431240859891640
限制与约定
| 测试点编号 | n≤ |
ai≤ |
type= |
|---|---|---|---|
|
1∼3 |
10 |
10 |
0 |
| 4∼6 |
50 |
103 |
|
| 7∼9 | 400 | 104 | |
|
10∼16 |
5000 | 105 | |
| 17∼22 | 5×105 | 106 | |
| 23∼25 | 4×107 | 109 |
1 |
对于所有测试数据满足type∈0,1,2≤n≤4×107,1≤ai≤109,1≤m≤105,1≤li≤ri≤109,0≤x,y,z,b1,b2<230
对于所有 type=0 的测试点,保证最终答案不超过 4×1018。
时间限制: 2s2s
空间限制: 1GB1GB
关于Hack数据
本题的hack数据对于type=0需满足2≤n≤500000,对于type=1需满足2≤n≤40,000,000。 ——matthew99